Algorytm dopasowania kroczącego (ang. Matching Pursuit, MP) to metoda analizy sygnałów, polegająca na znalezieniu reprezentacji sygnału wejściowego w dużym, redundantnym zbiorze arbitralnie dobranych funkcji. Przeszukiwanie takiego zbioru, zwanego słownikiem, dla znalezienia optymalnego dopasowania charakteryzuje się wysoką złożonością obliczeniową, jest tzw. problemem NP-trudnym. W 1993 roku Mallat i Zhang, jako rozwiązanie problemu, zaproponowali sub-optymalny, zachłanny algorytm iteracyjny, znany od tego czasu jako Matching Pursuit.

W swojej najprostszej formie, algorytm w każdym kroku wybiera ze słownika pojedynczą funkcję, zwaną atomem, taką która najlepiej dopasowuje się do sygnału resztkowego, pozostałego po odjęciu wyników poprzednich iteracji. Miarą dopasowania jest zazwyczaj iloczyn skalarny. Innymi słowy, w każdym kroku wybierana ze słownika jest taka funkcja, która tłumaczy możliwie dużą część pozostałej po poprzednich krokach energii sygnału. Udowodniono, że taka procedura jest zbieżna, a w jej wyniku otrzymuje się ważoną kombinację liniową wybranych funkcji z zadanego zbioru, zachowującą energię sygnału wejściowego. Główną zaletą MP jest możliwość użycia redundantnego słownika, co pozwala na bardzo elastyczną parametryzację struktur zawartych w sygnale.

Przy dekompozycji należy wybierać takie funkcje bazowe, których charakterystyka najbardziej odpowiada charakterystyce analizowanego sygnału. W przypadku sygnałów bioelektrycznych, w szczególności EEG, właściwe wydaje się wybranie funkcji Gabora (sinus o zadanej częstości modulowany obwiednią gaussowską), ze względu na optymalne właściwości w przestrzeni czas – częstość. Słownik można jednak skomponować dowolnie. Popularne jest wzbogacanie go o bazę funkcji sinusoidalnych, czy też delty Diraca. Niemniej jednak z powodzeniem można stosować słowniki złożone funkcji Bessela, Harra, czy wielomianów Czebyszewa. O wyborze funkcji słownika decyduje posiadana o dekomponowanym sygnale wiedza zewnętrzna.

Przykład działania

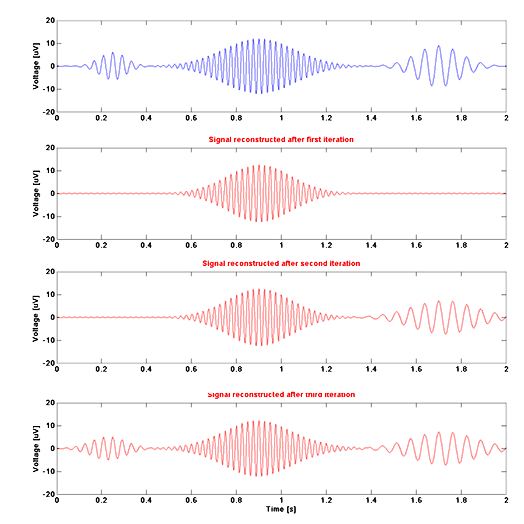
W celu przedstawienia działania algorytmu najłatwiej posłużyć się obrazem. Na rysunku obok przedstawiony jest symulowany sygnał (linia niebieska) oraz wynik jego parametryzacji (linie czerwone), kolejno po pierwszej, drugiej i trzeciej iteracji. Symulację przygotowano w środowisku Matlab, a sygnał zamodelowany został przy pomocy wbudowanej funkcji gausspulse(). Kolekcja funkcji wykorzystana w słowniku została jednak zbudowana od podstaw, dzięki czemu nie używano tych samych funkcji jednocześnie przy symulacji i wewnątrz słownika.

Program powinien w pierwszym kroku “wytłumaczyć” strukturę o największej energii i łatwo zauważyć, że tak jest w istocie. Funkcja Gabora znajdująca się po środku wymodelowanego sygnału charakteryzuje się największą energią i to właśnie do niej algorytm w pierszym kroku dopasował funkcję ze słownika. Następnie, druga iteracja skutkowała dopasowaniem fukcji po prawej stronie, a trzecia funkcji po lewej. Należy podkreślić, że funkcje narysowane kolorem czerwonym nie odpowiadają w stu procentach funkcjom zawartym w modelowanym sygnale. Są to po prostu najbliższe im odpowiedniki znajdujące się w słowniku, gdzie bliskość zdefiniowana została jako maksymalizacja iloczymu skalarnego.

Wynik działania algorytmu po przeprowadzeniu trzech iteracji przedstawiony jest na ostatnim panelu. Na pierwszy rzut oka, nie ma większych różnic między sygnałem wejściowym (panel górny, kolor niebieski), a sygnałem wyjściowym (panel dolny, kolor czerwony). W rzeczywistości jednak, można to porównać do różnic między grafiką rastrową, a grafiką wektorową – są ogromne. Tak, jak grafika rastrowa jest zbiorem pikseli o pewnych wartościach, tak też zamodelowany sygnał stanowił dyskretny zbiór próbek charakteryzujących się pewną amplitudą. Po wykonaniu rozkładu tego sygnału za pomocą MP, otrzymano zestaw kształtów (w tym przypadku trzech funkcji), które opisują ten zbiór próbek. Każda z wybranych funkcji posiada znane parametry, takie jak np. pozycja w czasie, amplituda, szerokość połówkowa, itd. Dlatego przyjęło się mówić, że MP umożliwia precyzyjną parametryzację struktur zawartych w sygnale.

A analogia do grafiki wektorowej? Sygnał wejściowy to zbiór próbek rejestrowanych ze stałym interwałem czasowym, na przykład co 0.01 [s], czyli 100 próbek w każdej sekundzie lub jeszcze inaczej – częstość próbkowania równa 100 [Hz]. Pomiędzy znanymi wartościami występują więc w sygnale “dziury” – odcinki czasu o niezmierzonej amplitudzie. Po zamianie na analityczne funkcje o znanych parametrach ten problem przestaje być istotny – można przybliżać bez utraty rozdzielczości, tak jak w przypadku grafiki wektorowej. Oczywiście, nie jest to sposób na obejście kryterium Nyquista, gdyż ono dotyka danych już w momencie ich rejestracji.

Przykład niedziałania

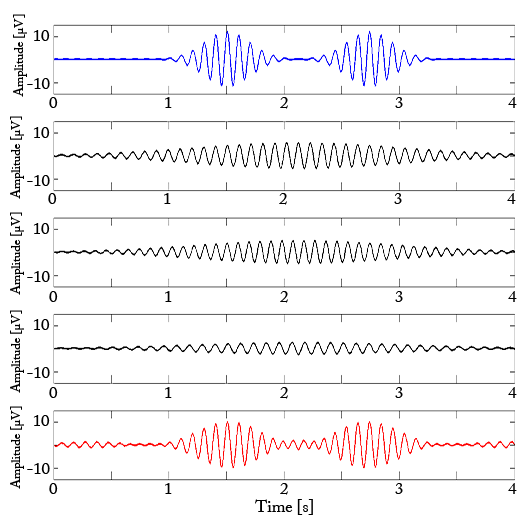
Wyobraźmy sobie złodzieja włamującego się do mieszkania. Złodziej przyniósł ze sobą plecak, w którym pragnie wynieść skradzione przedmioty. Plecak ma skończone wymiary i oczywistym jest, że wszystkie cenne przedmioty się w nim nie zmieszczą. Złodziej próbuje więc doprowadzić do sytuacji, w której ucieka z mieszkania z plecakiem wypełnionym rzeczami, których suma wartości jest jak największa. Należy zauważyć, że zagadnienie nie jest szczególnie trywialne. Poszukiwanie optymalnych przedmiotów jest wspomnianym już problemem NP-trudnym.

Teraz zamieńmy szybko nomenklaturę. Mieszkanie to słownik, a cenne przedmioty to funkcje w nim zawarte. Złodziej jest personifikacją algorytmu MP. Wartość przedmiotu-funkcji określona jest nie w dolarach, lecz w procencie wyjaśnianej przez tę funkcję energii zadanego sygnału. Jak zostało opisane na wstępie, algorytm MP nie podejmuje próby znalezienia optymalnego rozwiązania. Byłoby to bardzo czasochłonne. Zamiast tego, w każdym kroku wybiera po prostu najlepszą funkcję spośród aktualnie dostępnych. Mówiąc prościej, złodziej wybiera najdroższy przedmiot, jaki znajduje się w mieszkaniu i pakuje go do plecaka. Następnie sprawdza, czy w plecaku jest jeszcze miejsce i jeśli odpowiedź jest pozytywna, to znajduje kolejny, aktualnie najdroższy, dostępny przedmiot. Procedura jest powtarzana dopóki plecak nie zostanie całkowicie zapełniony.

Łatwo można dostrzec potencjalny problem takiego podejścia. Mianowicie, gdyby zlodziej porządnie przetrząsnął mieszkanie znalazłby biżuterię. Małe, lekkie przedmioty o sporej wartości. Znacznie przekraczającej wielki turecki dywan, z którym opuszcza mieszkanie. Dzieje się tak, gdyż każdy pojedynczy element biżuterii był od rzeczonego dywanu mniej warty, a poza dywanem, w plecaku nic się już nie chciało zmieścić. Jasne jest więc, skąd wzięło się określenie algorytm zachłanny.

Sytuację obrazuje rysunek po prawej. U góry, kolorem niebieskim przedstawiono symulowany sygnał, złożony z dwóch identycznych funkcji Gabora. Na kolejnych trzech panelach, kolorem czarnym przedstawione są wyniki trzech iteracji MP. Ostatni panel zawiera sygnał wyjściowy, przedstawiony w kolorze czerwonym – sumę wyników trzech przeprowadzonych kroków algorytmu. Funkcja znaleziona w pierwszym kroku z całą pewnością nie wyjaśnia poprawnie energii ani pierwszej, ani drugiej struktury widocznej w sygnale. Wyjaśnia jednak ponad 48% energii sygnału jako całości, co wystarcza, aby algorytm wybrał ją jako najlepszą. Tak wybrana funkcja jest następnie odejmowana od sygnału, co skutkuje zupełnym zafałszowaniem jego prawdziwej natury. Kolejne kroki algorytmu muszą więc skutkować równie błędnymi wynikami. Niemniej jednak po złożeniu wyników kolejnych iteracji w całość, otrzymuje się kształt podobny do sygnału wejściowego. Nie można jednak mówić o jego właściwej parametryzacji.

Implementacje MP (do których się przyznaję)

Istnieje wiele implementacji algorytmu MP. Metodologia jest rozwijana w Zakładzie Fizyki Biomedycznej Uniwersytetu Warszawskiego na przestrzeni wielu ostatnich lat. MP jest również rozwijane przez inne ośrodki badawcze, rozsiane po całym świecie. Z powodzeniem stosowano MP w zagadnieniach takich jak: opis parametryczny EEG snu, analiza zjawisk ERD/ERS, parametryzacja sygnału na potrzeby rozwiązania problemu odwrotnego w EEG.

Matlab:

Kod MP w środowisku Matlab od samego początku pisany był z myślą o użytkownikach pakietu EEGLAB. Instalacja, jeśli tak można tę procedurę nazwać, sprowadza się do przekopiowania plików programu do katalogu “plugins”, znajdującego się wewnątrz głównej instalacji toolbox’a. Program można oczywiście uruchomić niezależnie, jednak nie będzie to wygodne w dłuższej perspektywie czasowej. Początkowo nie uświadomiłem sobie, jak bardzo zintegruję implementację MP ze strukturą i filozofią działania EEGLAB’a, a później nie miałem już chęci (ani potrzeby, szczerze mówiąc) tego zmieniać.

Repozytorium GIT: matlab-matchingPursuit
Status: Work In Progress, Usable
Zależności:

• Matlab 2011a lub nowszy
• Matlab Signal Processing Toolbox
• Eeglab 11_0_4_3b lub nowszy

Python:

Imlementację matlabową pisałem niejako raczkując w świecie programowania. Nie uważam, żeby kod został napisany bardzo źle, niemniej jednak dziś niemal wszystko zaprogramowałbym inaczej. Z taką właśnie myślą zabrałem się za napisanie programu MP w języku Python. Rzeczy, które teraz zaprogramowałbym inaczej jest nadal sporo, niemniej jednak z jądra aplikacji jestem całkiem zadowolony. Program czeka dalsza rozbudowa (plan na początek roku 2016), więc jest jeszcze szansa na poprawę jakości kodu i zmiany na lepsze.

Repozytorium GIT: python-matchingPursuit
Status: Work In Progress, Usable
Zależności:

• Python 2.7
• Numpy
• SciPy
• Pandas
• MatPlotLib